PPO: Proximal Policy Optimization Algorithms 近端策略优化算法

• paper: 1707.06347
• Proximal Policy Optimization Algorithms 近端策略优化算法

“近端 proximal” 主要体现在对策略更新幅度的限制，保证新策略和旧策略之间较为 “接近”，这是算法的核心特性。

简介

近端策略优化（PPO）算法旨在结合信任区域策略优化（TRPO）的数据效率和可靠性能，同时使用更简单的一阶优化方法。

其核心在于提出了一个带有裁剪概率比（clipped probability ratios）的目标函数，以此对策略性能进行悲观估计（pessimistic estimate i.e. lower bound）。

传统策略优化

论文中提到了以下两种传统策略优化作为 background：

1. 在标准策略梯度方法中，目标是最大化策略梯度估计器对应的目标函数 $$L^{PG}(\theta)=\hat{\mathbb{E}}_{t}\left[\log \pi_{\theta}\left(a_{t} | s_{t}\right) \hat{A}_{t}\right]$$

• $\pi_{\theta}$是随机策略，$\hat{A}_{t}$是优势函数在时刻$t$的估计值。

2. 在信任区域策略优化（TRPO）中，TRPO 会最大化一个替代目标函数$L^{CPI}(\theta)$ ， $$L^{CPI}(\theta)=\hat{\mathbb{E}}_{t}[r_t(\theta)\hat{A}_t]$$

• $r_t(\theta)=\frac{\pi_{\theta}(a_t | s_t)}{\pi_{\theta_{old}}(a_t | s_t)}$表示概率比率
• $\hat{A}_t$是优势函数估计值

然而，如果没有约束条件，对$L^{CPI}$进行最大化会导致策略更新幅度过大，影响学习的稳定性。

原理

Clipped Surrogate Objective

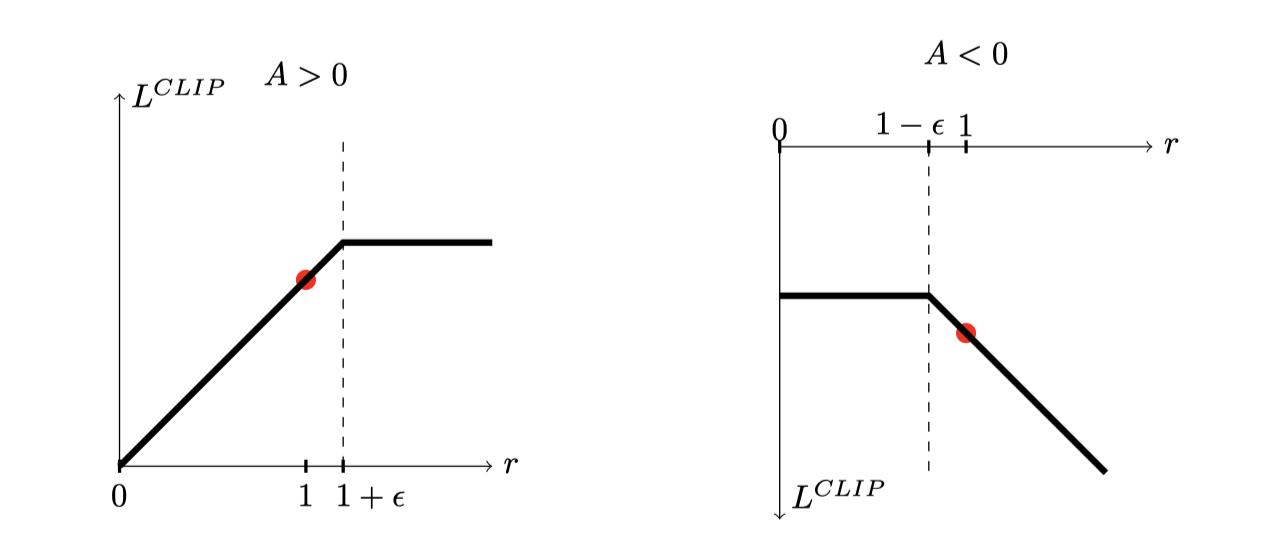
Clipped Surrogate Objective（裁剪替代目标函数）是 PPO 算法中的关键概念，旨在改进传统策略优化中可能出现的策略更新幅度过大的问题，使策略学习更加稳定和有效。

PPO提出的裁剪替代目标函数为

• $\epsilon$是超参数，常取$0.2$

重点在于裁剪函数 $\text{clip}(r_t(\theta),1 - \epsilon,1 + \epsilon)$，它将概率比率 $r_t(\theta)$ 限制在 $[1 - \epsilon,1 + \epsilon]$ 区间内 - 如果 $r_t(\theta)$ 超出区间端点，则裁剪为duan端点；在区间内则保持不变

$L^{CLIP}(\theta)$ 的 min 函数中：

• 参数一是 TRPO 中的目标函数 $L^{CPI}$
• 参数二是代入裁剪过的概率比率的目标函数

取两者最小值，使得 $L^{CLIP}(\theta)$ 成为未裁剪目标函数 $L^{CPI}$ 的下限，即文中提到的 pessimistic 的界限。

Adaptive KL Penalty Coefficient

除了裁剪概率比率，PPO 还提出了另一种方法，自适应 KL 散度惩罚系数，其目标函数为：

$L^{PENALTY}(\theta)=\hat{\mathbb{E}}_{t}\left[r_{t}(\theta) \hat{A}_{t}-\beta KL\left[\pi_{\theta_{old}}\left(\cdot | s_{t}\right), \pi_{\theta}\left(\cdot | s_{t}\right)\right]\right]$

• $\beta$ 是一个系数，需要动态调整
• $KL\left[\pi_{\theta_{old}}\left(\cdot | s_{t}\right), \pi_{\theta}\left(\cdot | s_{t}\right)\right]$ 是新旧策略在状态$s_t$下的KL散度

通过在目标函数中加入KL散度惩罚项，限制策略更新的幅度。

实现

PPO算法的具体实现步骤如下：

1. 数据采样：使用当前策略$\pi_{\theta}$与环境进行交互，收集一批轨迹数据$\{(s_t, a_t, r_t)\}$，其中$s_t$是状态，$a_t$是动作，$r_t$是奖励。
2. 优势估计：计算每个时间步的优势函数估计值$\hat{A}_{t}$。常见的方法有广义优势估计（Generalized Advantage Estimation，GAE）等。
3. 目标函数优化：根据选定的目标函数（如$L^{CLIP}$或$L^{PENALTY}$），使用随机梯度上升算法对策略参数$\theta$进行多轮次（多个epoch）的小batch更新。例如，对于PPO中的CLIP方法，通过最大化$L^{CLIP}(\theta)$来更新$\theta$。
4. 参数更新：在完成对采样数据的多轮优化后，更新策略参数$\theta$，并重复上述步骤进行下一轮的采样和优化。

优势

PPO算法具有以下显著优势：

1. 实现简单：相较于TRPO，PPO无需复杂的二阶优化方法（如共轭梯度算法），仅使用一阶优化（如随机梯度上升），降低了实现难度和计算复杂度。
2. 数据效率高：通过 clipped 或 KL散度惩罚项 的方法，PPO能够在有限的样本数据上进行有效的策略更新，避免了策略更新幅度过大导致的性能波动，提高了数据的利用效率。
3. 通用性强：PPO适用于各种不同的强化学习任务，包括连续控制任务和离散动作空间任务（如Atari游戏）。在实验中，它在多个基准任务上表现出色，能够在不同的环境中取得较好的性能。
4. 样本复杂度低：与其他在线策略梯度方法相比，PPO在较少的样本数量下就能达到较好的性能，减少了与环境交互的次数，从而节省了训练时间和资源。