cssclasses:

smalli number headings:

ML Framework

target: looking for function

function with unknown
define loss
optimization

function with unknown

Hard Sigmoid 是常见的目标 function。

可以用 Sigmoid Function 逼近 Hard Sigmoid

多个 sigmoid 合成 red curve

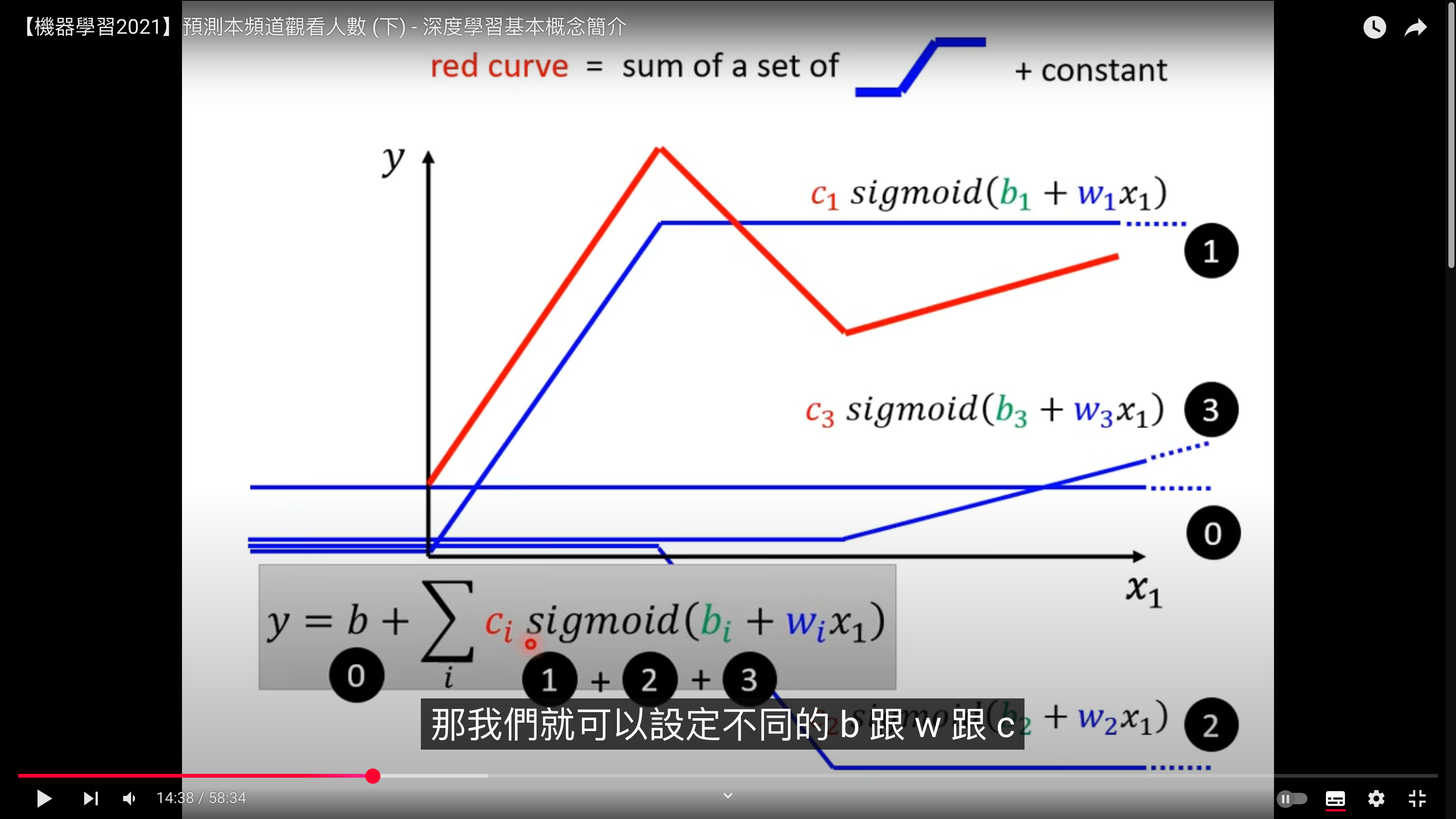
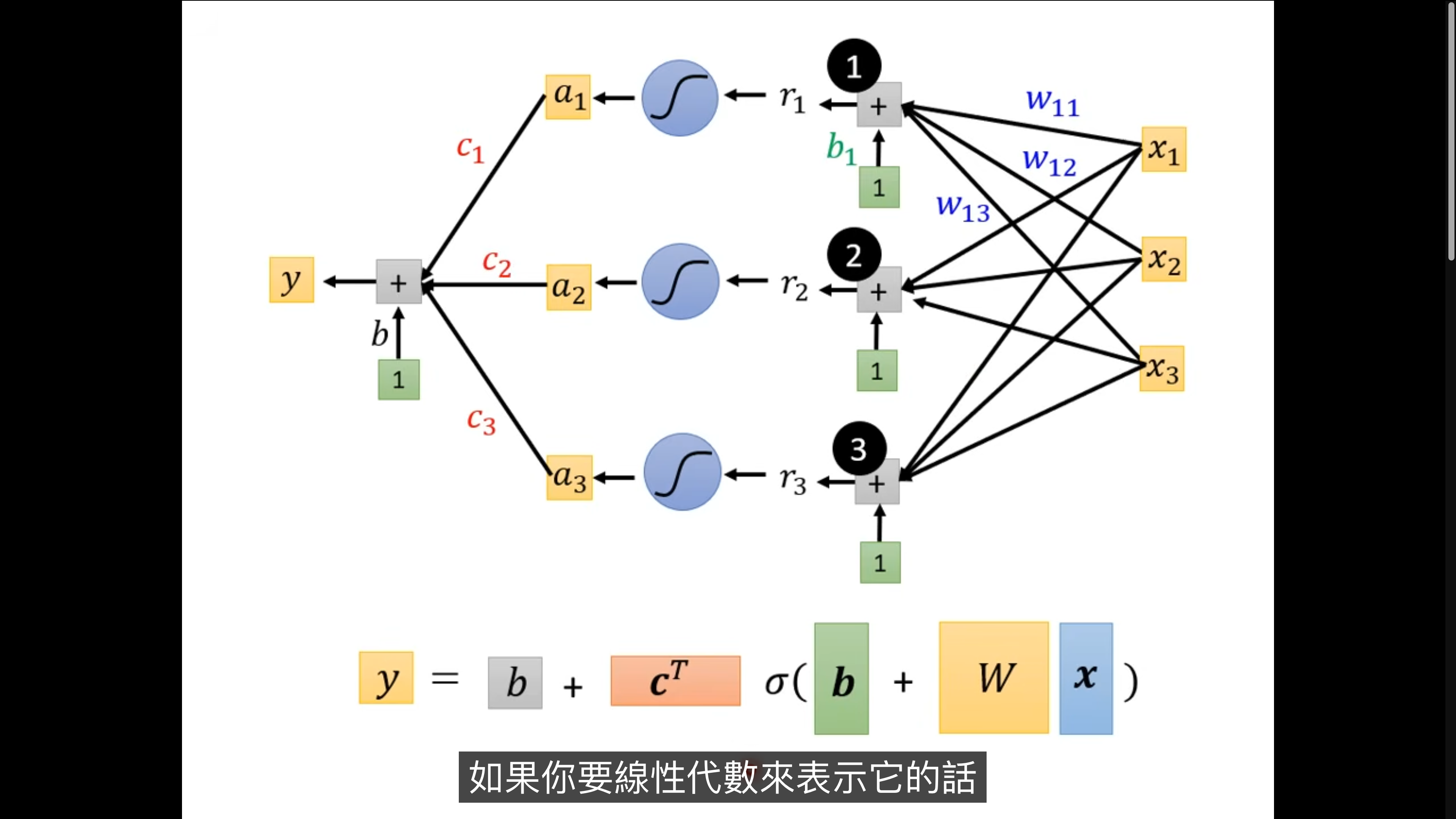
最终的 function with unknown

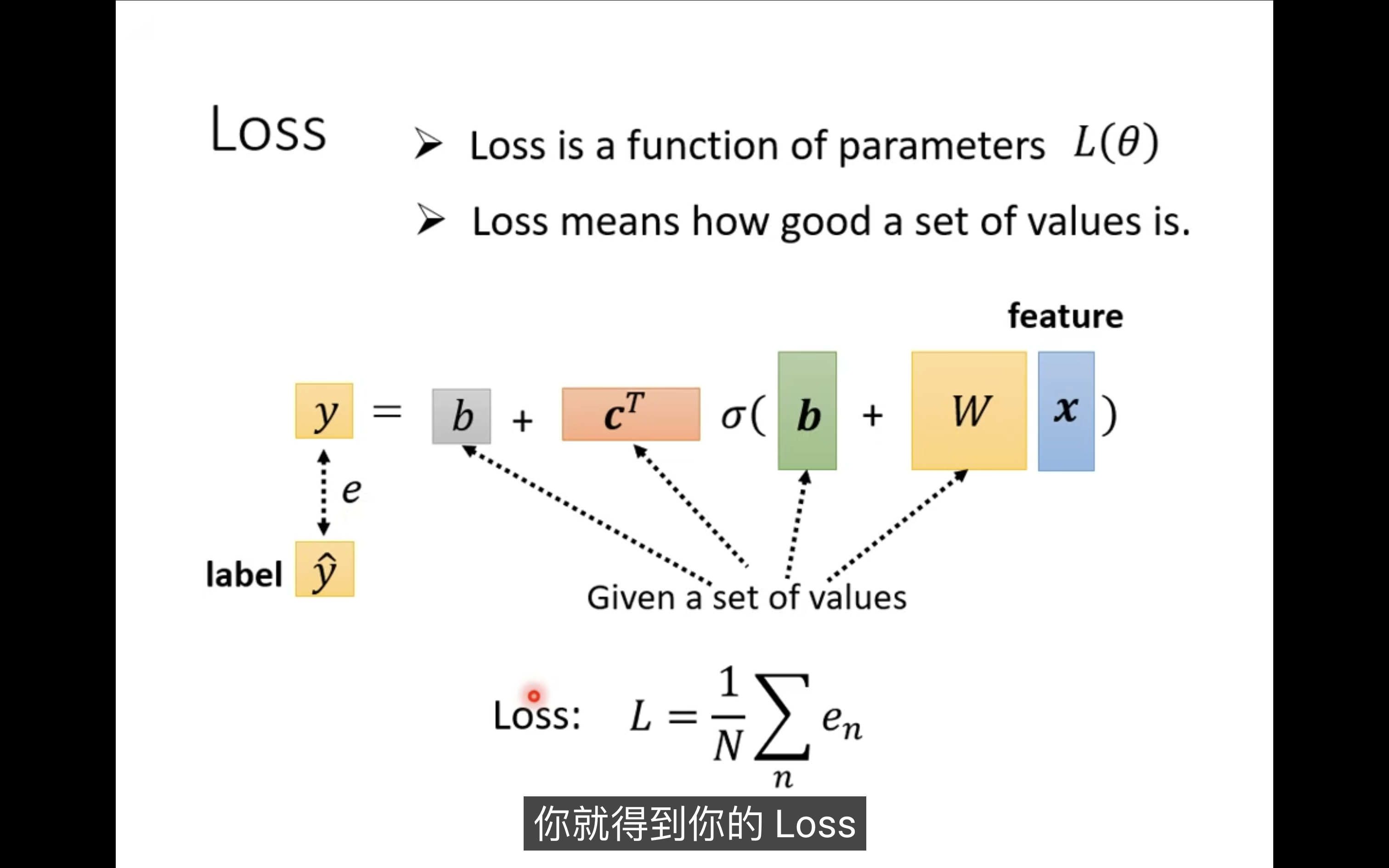
loss

optimize

不断更新 gradient

总的数据集会分成很多 batch：

遍历所有batch称为一次epoch
update指更新一次batch

more layers

可以把模型进一步改成多层：

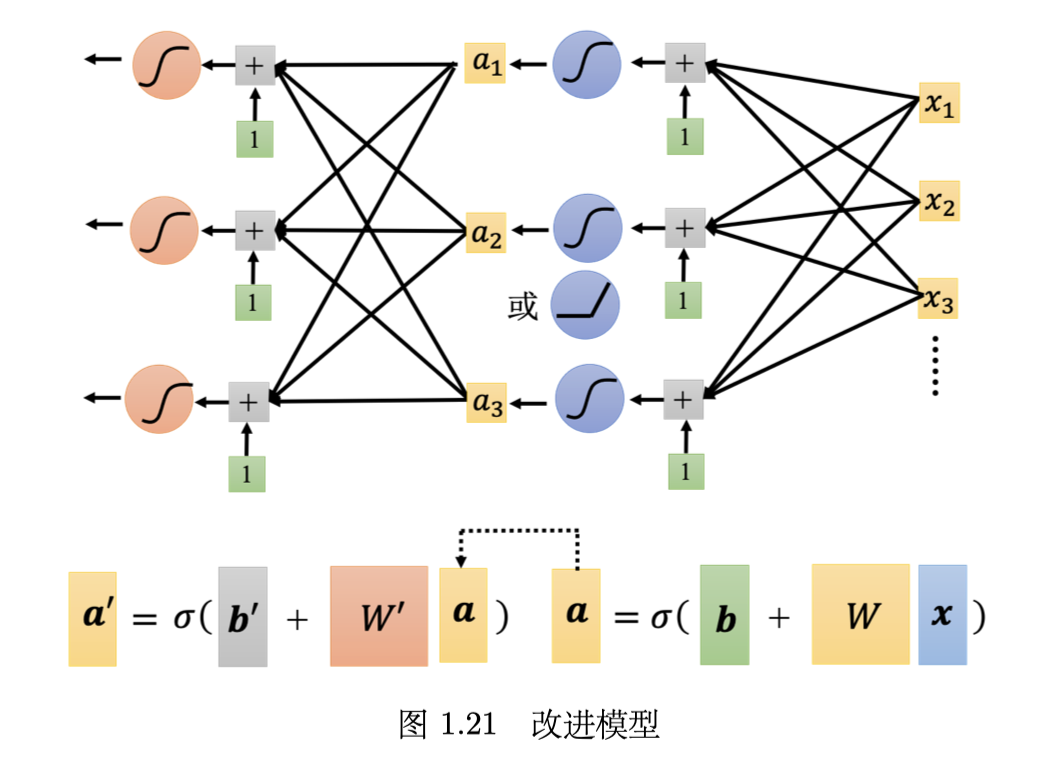
每一层都是一个 Sigmoid 或 ReLU 的 function，称为神经元（neuron），很多的神经元称为神经网络（neural network）。

神经网络不是新的技术，80、90 年代就已经用过了，后来为了要重振神经网络的雄风，所以需要新的名字。每一层，称为隐藏层（hidden layer），很多的隐藏层就“深”，这套技术称为深度学习。

但是层数不一定越深越好，可能会出现过拟合 overfitting 的问题：

General Guidance

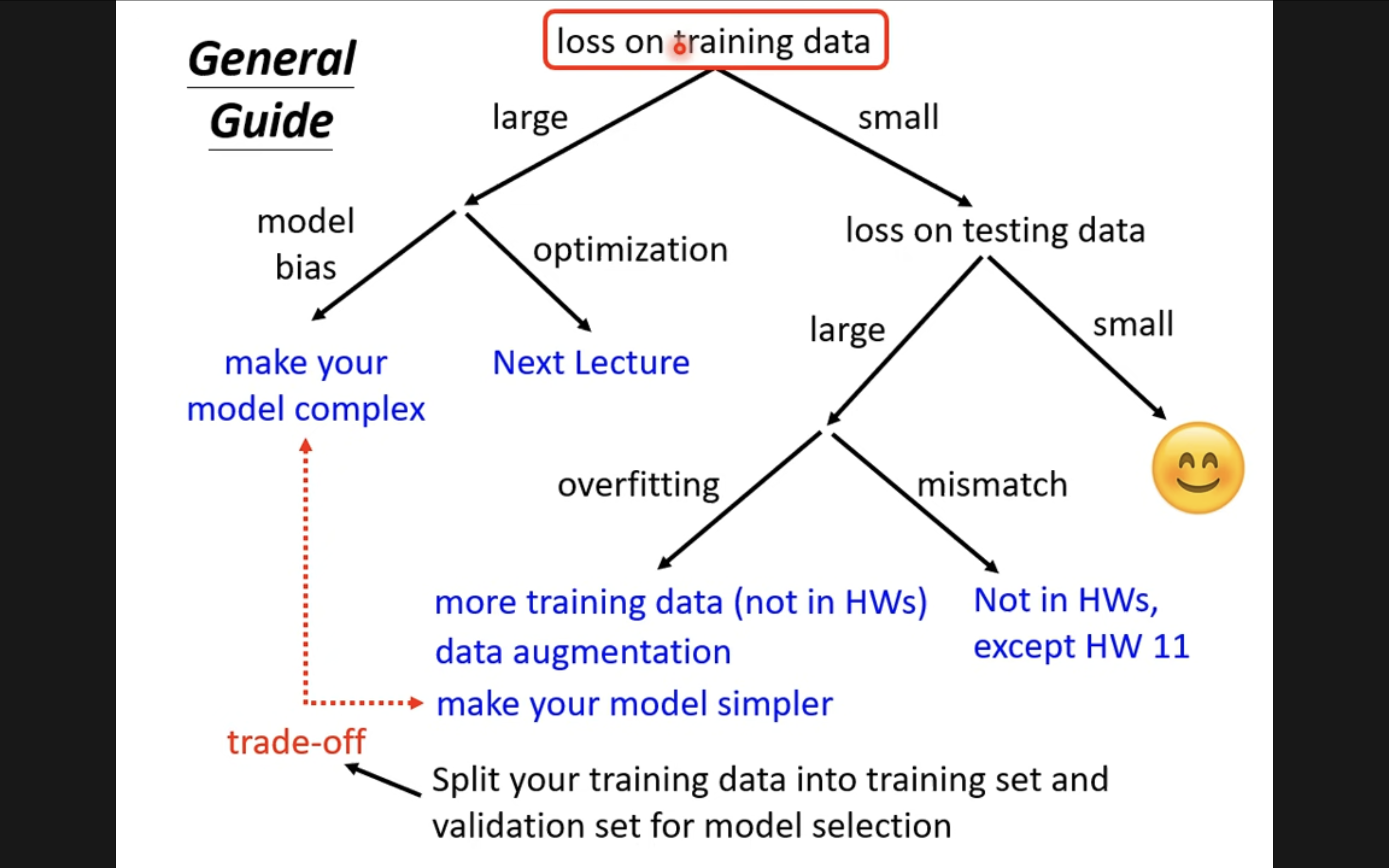
model bias

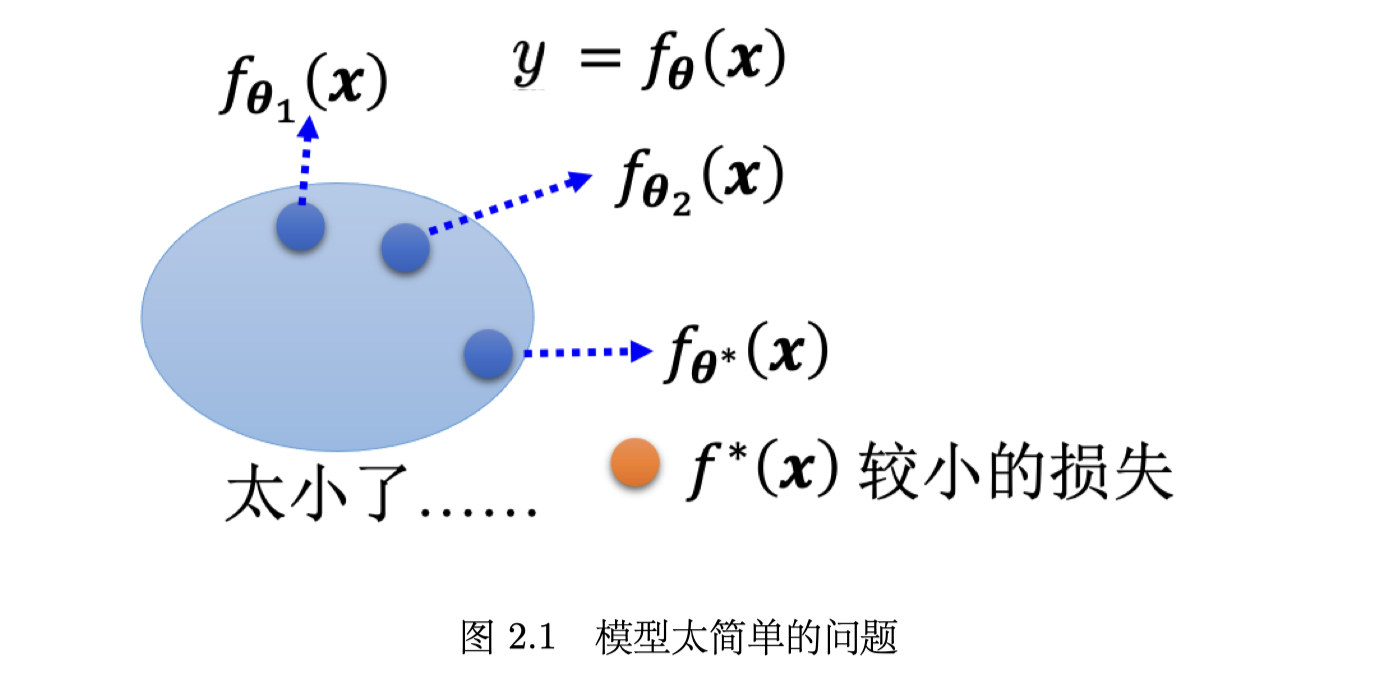
假设模型过于简单，一个有未知参数的函数代 θ1 得到一个函数 fθ1(x)，同理可得到另一个函数 fθ2(x)，把所有的函数集合起来得到一个函数的集合。但是该函数的集合太小了，没有包含任何一个函数，可以让损失变低的函数不在模型可以描述的范围内。在这种情况下，就算找出了一个 θ∗ ，虽然它是这些蓝色的函数里面最好的一个，但损失还是不够低。

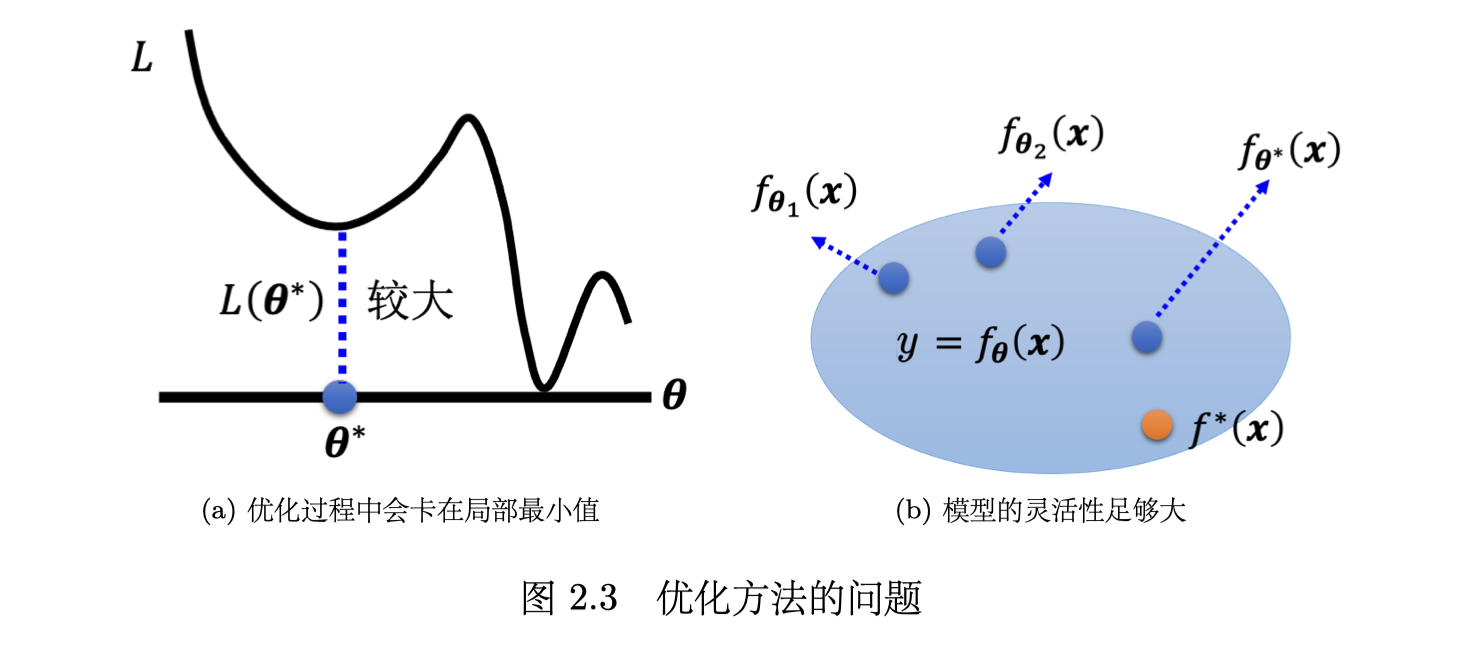
optimization

一般只会用到梯度下降进行优化，这种优化的方法很多的问题。比如(a)可能会卡在局部最小值的地方，无法找到一个真的可以让损失很低的参数。

overfitting

过拟合的表现为：训练数据上面的损失小，测试数据上的损失大。

例子：模型过于灵活

在这 3 个蓝点（训练数据）上面，要让损失低，所以模型的这个曲线会通过这 3 个点，但是其它没有训练集做为限制的地方，因为它的灵活性很大，所以模型可以变成各式各样的函数，没有给它数据做为训练，可以产生各式各样奇怪的结果（“随意”）。

最终，表现为训练数据loss为0，测试数据loss很大。

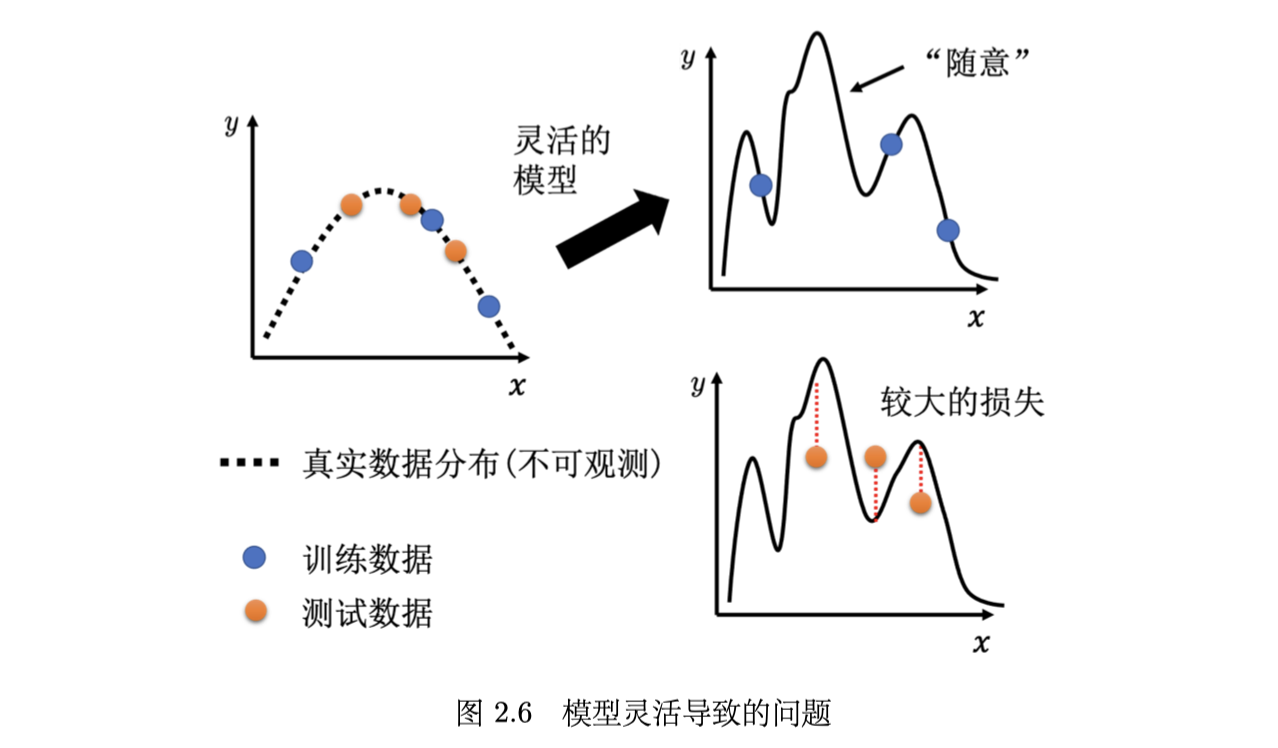
可以用数据增强和限制模型的方法，降低 overfitting

data augmentation

根据问题的理解创造出新的数据。举个例子，在做图像识别的时候，常做的一个招式是，假设训练集里面有某一张图片，把它左右翻转，或者是把它其中一块截出来放大等等。

limitation

限制模型，让模型不要有过大的灵活性。

减少模型参数：对于神经网络，可以减少每层的参数
减少数据特征值
早停（early stopping）、正则化（regularization）和丢弃法（dropout method）

cross validation

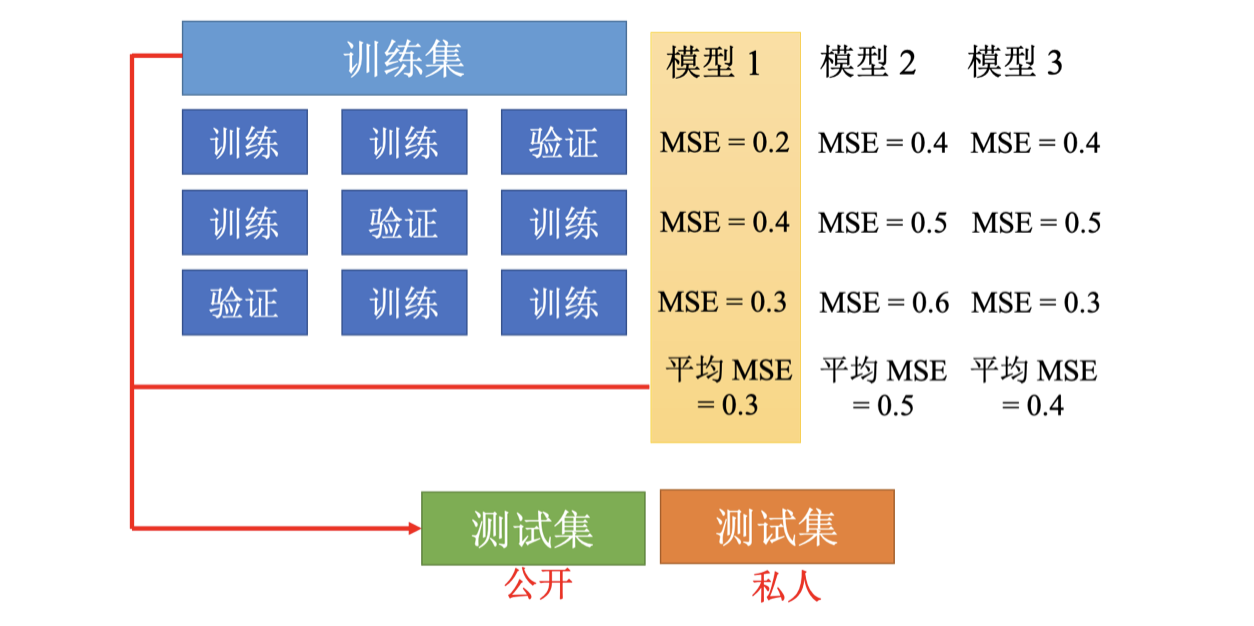
交叉验证 Cross Validation 是为了避免在测试集上面过拟合。

k 折交叉验证就是先把训练集切成 k 等份。在这个例子，训练集被切成 3 等份，切完以后，拿其中一份当作验证集，另外两份当训练集。

这件事情要重复 3 次：第一份第 2 份当训练，第 3 份当验证；第一份第 3 份当训练，第 2 份当验证；第 1 份当验证，第 2 份第 3 份当训练。

mismatch

不匹配，简单理解就是一种反常的情况发生了。

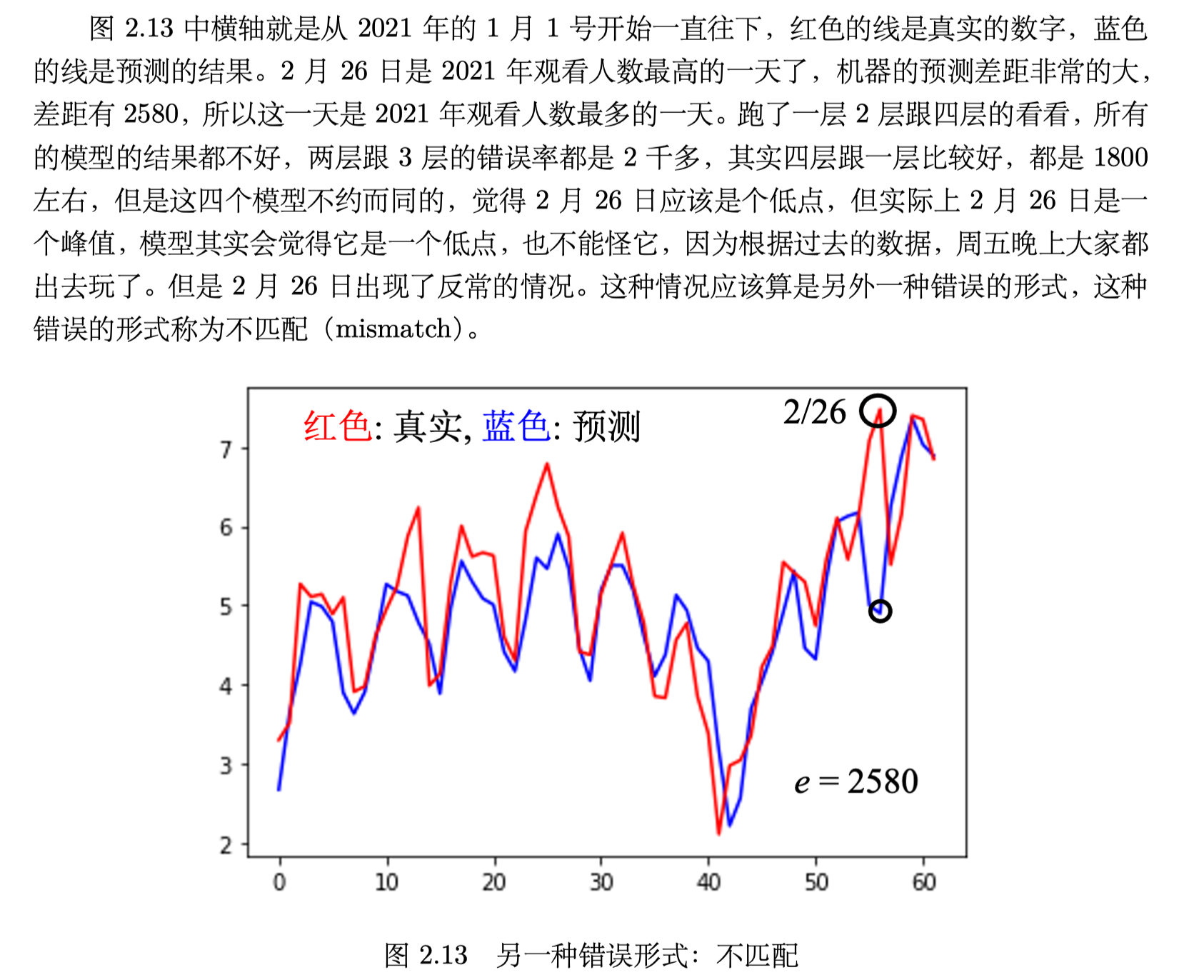
而且，增加数据也不能让模型做得更好，到底有没有mismatch，要看人对数据本身的理解。

Deep Learning Basics

local minima and saddle point

local minima 是局部极小值
saddle point 是鞍点，不是极小，可以向其他方向 escape

这两者一般统称为 critical point 临界点。

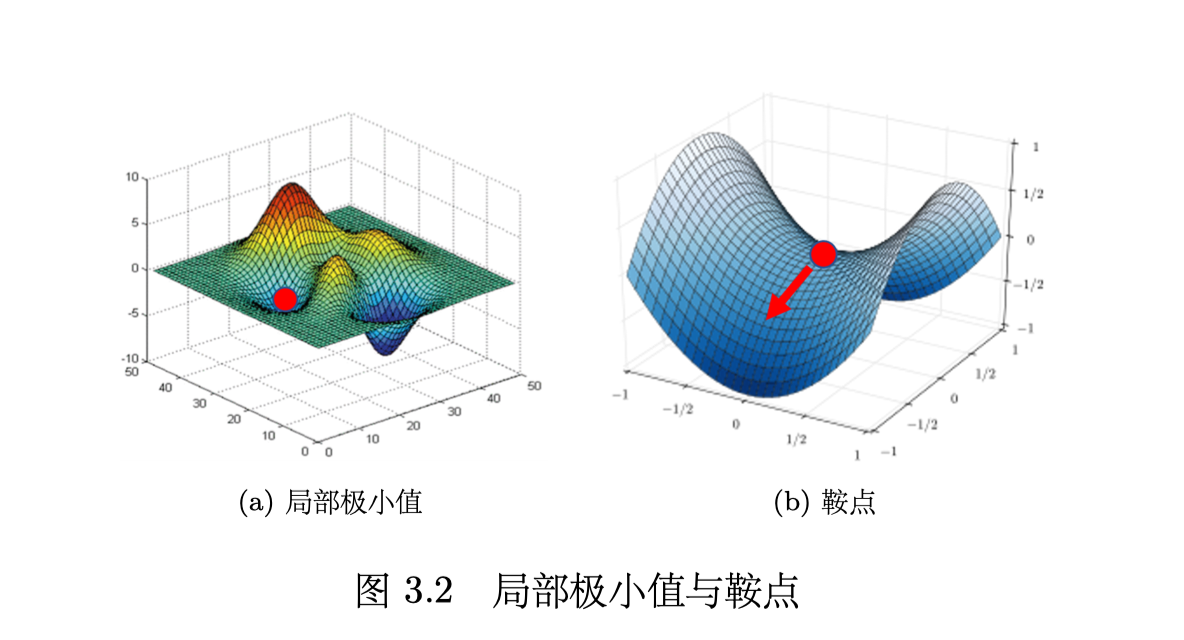
determining the types of critical point

损失函数可由于泰勒级数近似为：

L({\theta}) \approx L\left({\theta}'\right) + \left({\theta} - {\theta}'\right)^{\mathrm{T}} {g} + \frac{1}{2} \left({\theta} - {\theta}'\right)^{\mathrm{T}} {H} \left({\theta} - {\theta}'\right)

其中，H 里面放的是 L 的二次微分，可以通过 $\frac{1}{2} \left({\theta} - {\theta}'\right)^{\mathrm{T}} {H} \left({\theta} - {\theta}'\right)$ 的正负判断是否是极小值。

batch size

大的批量往往在训练的时候结果比较差，小的批量优化的结果是比较好的，这个是优化的问题。

local minima 也分好坏，如下图：

flat minima 是好的
sharp minima 是坏的

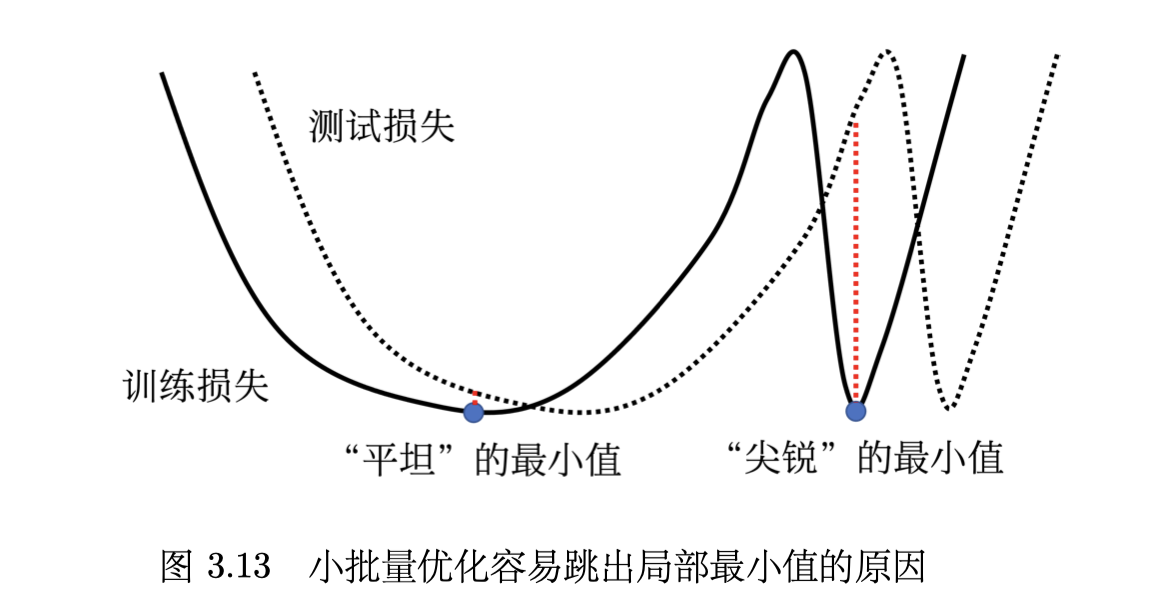
评价 local minima 好坏的根本在于：

train 和 test 的 loss 一般有一些差别
两者的 flat minima 往往很接近
但是 sharp minima 很有可能会有很大差别

批量大小对梯度下降法的影响的直观理解：

大的批量大小会让我们倾向于走到“峡谷”里面，而小的批量大小倾向于让我们走到“盆地” 里面。小的批量有很多的损失，其更新方向比较随机，其每次更新的方向都不太一样。即使 “峡谷”非常窄，它也可以跳出去，之后如果有一个非常宽的“盆地”，它才会停下来。

momentum method

动量法是另一种可以对抗 local minima 和 saddle point 的方法

假设误差表面就是真正的斜坡，参数是一个球，把球从斜坡上滚下来，如果使用梯度下降，球走到或鞍点就停住了。

但是在物理的世界里，一个球如果从高处滚下来，就算滚到鞍点或局部最小值点，因为惯性的关系它还是会继续往前走。如果球的动量足够大，其甚至翻过小坡继续往前走，它并不一定会被鞍点或局部最小值点卡住，如果将其应用到梯度下降中，这就是动量。

引入动量后，可以从两个角度来理解动量法：

一个角度是动量是梯度的反方向加上前一次移动的方向
另外一个角度是当加上动量的时候，更新的方向不是只考虑现在的梯度，而是考虑过去所有梯度的总和

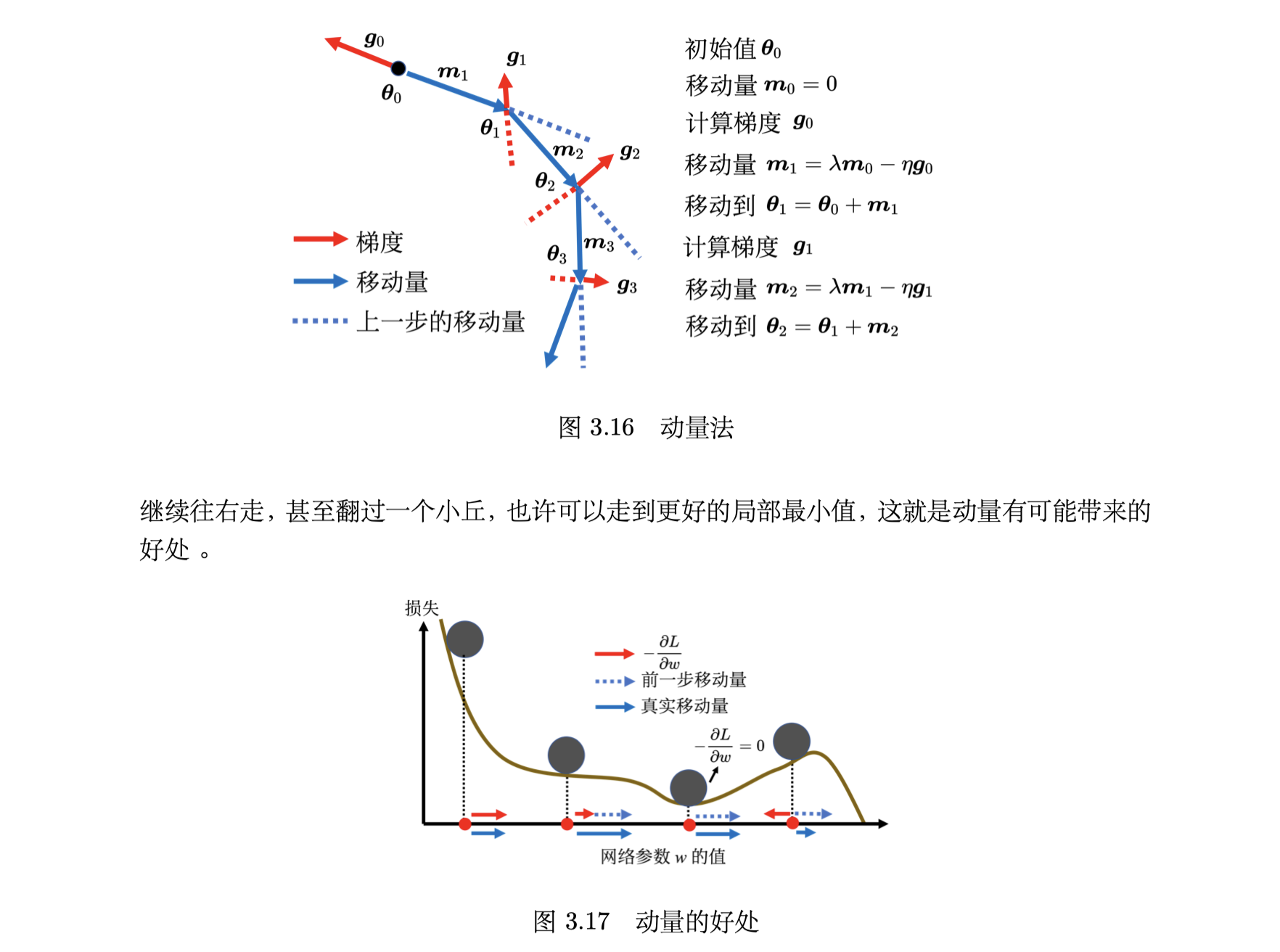
其中 η 是学习率， λ 是前一个方向的权重参数，是需要调的。

adaptive learning rate

不同学习率：

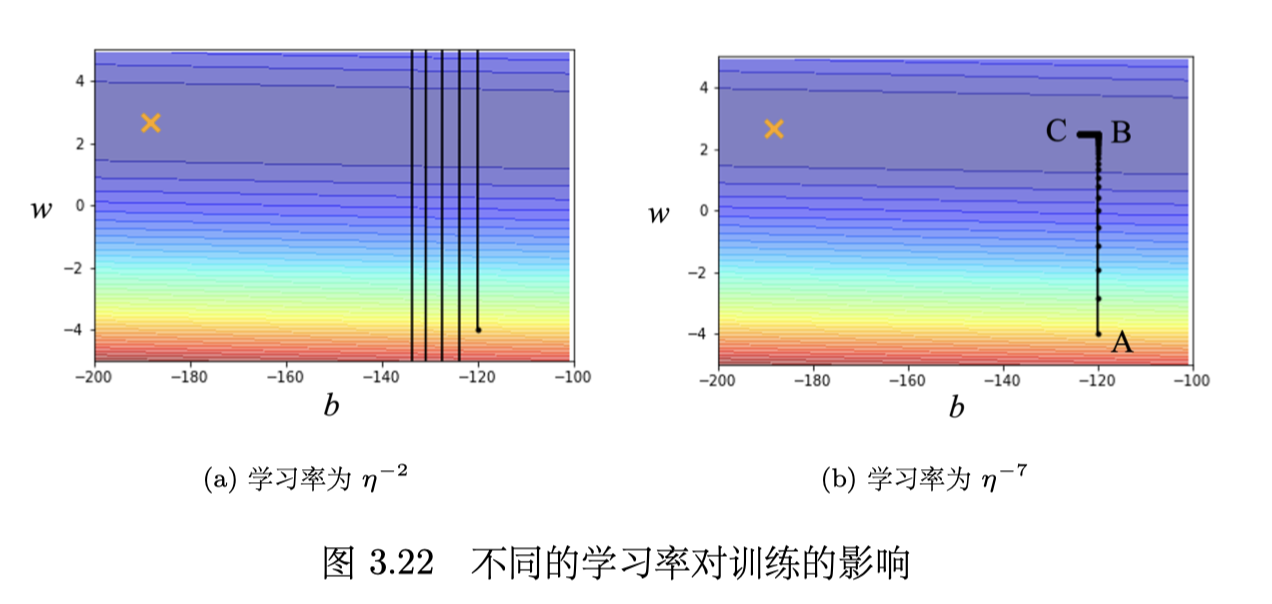
图中误差表面的最低点在叉号处
学习率太大会导致训练时参数不断震荡，如图a
学习率变小可以解决震荡的问题，但是在左拐以后，BC 段的坡度已经非常平坦了（指梯度很小），这种小的学习率无法再让参数前进到目标位置，如图b

AdaGrad

AdaGrad（Adaptive Gradient）是典型的自适应学习率方法，其能够根据梯度大小自动调整学习率。AdaGrad 可以做到梯度比较大的时候，学习率就减小，梯度比较小的时候，学习率就放大。

原始的梯度下降更新某个参数 θ 的过程为（学习率固定）：

\boldsymbol{\theta}_{t + 1}^i \leftarrow \boldsymbol{\theta}_{t}^i - \eta \boldsymbol{g}_{t}^i

AdaGrad 的更新过程，学习率不再固定： $\boldsymbol{\theta}_{t + 1}^i \leftarrow \boldsymbol{\theta}_{t}^i - \frac{\eta}{\sigma*{t}^i} \boldsymbol{g}*{t}^i$

新引入的符号的说明，要点就是学习率就变得参数相关（parameter dependent）：

最终自适应的效果如下：

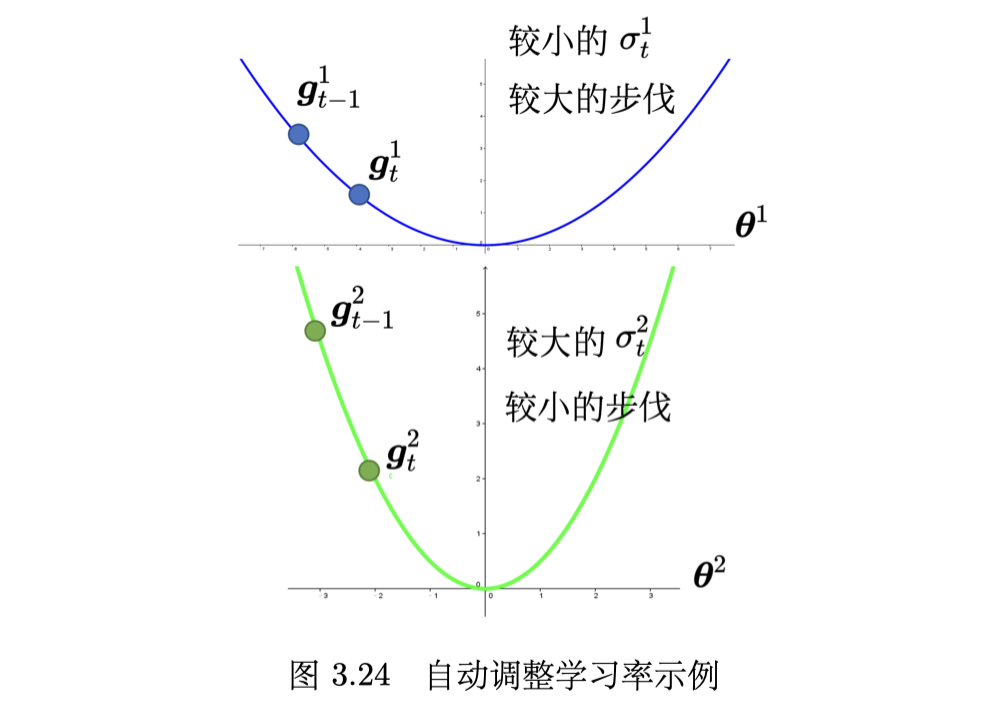
RMSProp

RMSprop（Root Mean Squared propagation）是 Geoffrey Hinton 在 Coursera 上的深度学习的课程中提到的，没有论文，属于黑科技了...

RMSProp 第一步跟 Adagrad 的方法是相同的，即

\sigma_{0}^{i} = \sqrt{\left(g_{0}^{i}\right)^{2}} = \vert \boldsymbol{g}_{0}^{i}\vert

第二步更新过程为

\boldsymbol{\theta}_{2}^{i} \leftarrow \boldsymbol{\theta}_{1}^{i}-\frac{\eta}{\sigma_{1}^{i}}\boldsymbol{g}_{1}^{i} \quad \sigma_{1}^{i}=\sqrt{\alpha\left(\sigma_{0}^{i}\right)^{2}+(1 - \alpha)\left(\boldsymbol{g}_{1}^{i}\right)^{2}}

这里额外引入了一个超参数 α，且 0 < α < 1。

通过 α 可以在计算算均方根的时候，调整现在这个梯度的重要性。如果 α 设很大趋近于 1，代表 g1i 比较不重要，之前算出来的梯度比较重要。

而上一节的 Adagrad 则是每一个梯度都有同等的重要性，不够灵活。

Adam

Adam（Adaptive moment estimation）是最常用的优化策略/优化器 optimizer

Adam 可以看作 RMSprop 加上动量，其使用动量作为参数更新方向，并且能够自适应调整学习率。PyTorch 里面已经写好了 Adam 优化器，这个优化器里面有一些超参数需要人为决定，但是往往用 PyTorch 预设的参数就足够好了。

learning rate scheduling

学习率调度（learning rate scheduling）中 η 跟时间有关，最常见的策略是学习率衰减（learning rate decay）。

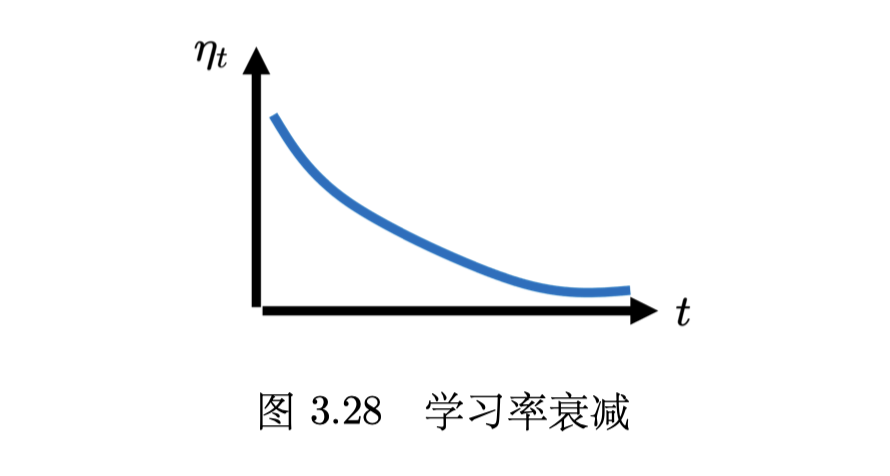
还有一种策略是 warmup，即先上升一小段，到达一定值再下降。

BERT 和 Transformer 的训练都使用了 warmup，但 warmup 比较像一个 trick，没有人严谨解释为什么，一个可能的原因是：统计的结果需要足够多的数据才精准，一开始统计结果 σ 是不精准的，所以需要先上升一段时间，以收集有关 σ 的统计数据。

classfication

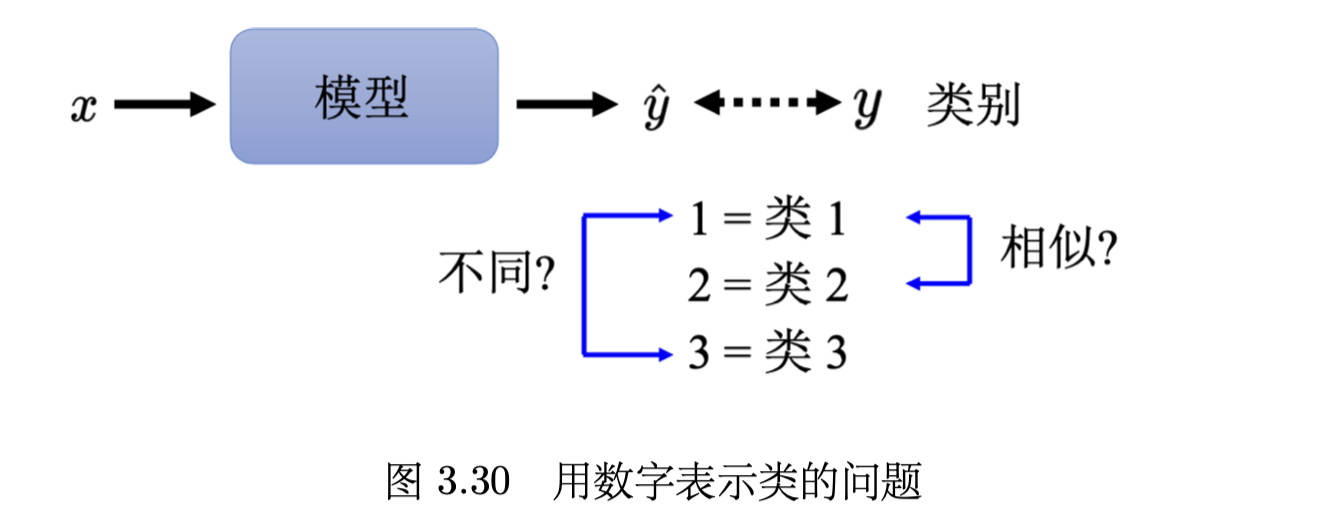
Class as one-hot vector

使用 one-hot vector 每个vector的距离是一样的，直接用数字 1 2 3 的话，三者之间的距离不同。

李宏毅2022机器学习课程笔记